PX153 - J8 - sine and cosine series

it is possible to use only sines or cosines:
cosine series:

f (x) = \frac{a_{0}}{2} + \sum_{n = 1}^{\infty} a_{n} \cos (\frac{n π x}{L})

for $x \in [0, L)$

sine series:

f (x) = \sum_{n = 1}^{\infty} b_{n} \sin (\frac{n π x}{L})

for $x \in [0, L)$

the only differences with full intervals:
- $a_{n}, b_{n}, a_{0}$ coefficients will be calculated slightly differently
- periodic extensions outside of $x \in [0, L)$ will be different
- convergence properties

periodic extensions

can be evaluated $\forall x$
periodic over $2 π$ , but only represent $f (x)$ in the interval $[0, L)$
sine (odd) series has antisymmetric periodic extensions, and cosine (even) series has symmetric periodic extensions

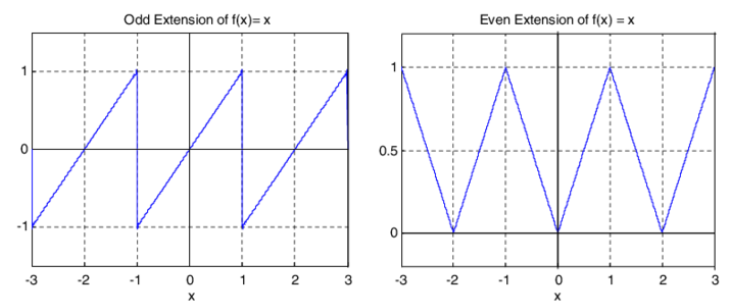
finding the coefficients

multiply by $\cos (\frac{n^{'} π x}{L})$ , then by $\sin (\frac{n^{'} π x}{L})$ , and integrate from $0$ to $L$
eg: $b_{n}$ for sine series, taking the general case, $x \in [0, L)$

\begin{aligned} \int_{0}^{L} f (x) \sin (\frac{n^{'} π x}{L}) \\ = \sum_{n} b_{n} \int_{0}^{L} \sin (\frac{n π x}{L}) \sin (\frac{n^{'} π x}{L}) d x \\ l e t x^{'} = \frac{π x}{L} ⟹ d x^{'} = \frac{π}{L} d x \\ = \sum b_{n} \int_{0}^{π} \frac{L}{2 π} (\cos ((n - n^{'}) x^{'}) - \cos ((n + n^{'}) x^{'})) d x^{'} \\ = \sum_{n \neq n^{'}} \frac{b_{n} L}{2 π} {[\frac{\sin ((n - n^{'}) x^{'})}{n - n^{'}} - \frac{\sin ((n - n^{'}) x^{'})}{n + n^{'}}]}_{0}^{π} \\ + \frac{b_{n} L}{2 π} [x^{'} - \frac{\sin ((n + n^{'}) x)}{n + n^{'}}] \\ = \frac{b_{n} L}{2} \end{aligned}

b_{n} = \frac{2}{L} \int_{0}^{L} f (x) \sin (\frac{n^{'} π x}{L}) d x

similarly,

\begin{aligned} a_{n} & = \frac{2}{L} \int_{0}^{L} f (x) \cos (\frac{n^{'} π x}{L}) d x \\ a_{0} & = \frac{2}{L} \int_{0}^{L} f (x) d x \end{aligned}

eg: $f (x) = \cos x$ for $x \in [0, π)$
- cosine series: $f (x) = \cos (x)$
- sine series: point-wise convergence

\begin{aligned} b_{n} & = \frac{2}{π} \int \cos x \sin (n x) d x \\ = \frac{2}{π} \int_{0}^{π} \frac{1}{2} (\sin ((n + 1) x) + \sin ((n - 1) x)) d x \\ = \frac{1}{π} {[- \frac{\cos ((n + 1) x)}{n + 1} - \frac{\cos ((n - 1) x)}{n - 1}]}_{0}^{π} \\ = \frac{1}{π} [\frac{- (- 1)^{n + 1} + 1}{n + 1} + \frac{- (- 1)^{n - 1} + 1}{n - 1}] \\ = \frac{1}{π} [\frac{(- 1)^{n} + 1}{n + 1} + \frac{(- 1)^{n} + 1}{n - 1}] \end{aligned}

- for $n \in e v e n :$

b_{n} = \frac{1}{π} (\frac{2}{n + 1} + \frac{2}{n - 1}) = \frac{4 n}{n^{2} - 1} (\frac{1}{π})

- for $n \in o d d :$
$$b_{n}=0$$

\begin{aligned} \cos x & = \frac{1}{π} (\frac{8}{3} \sin (2 x) + \frac{16}{15} \sin (4 x) + . . .) \\ = \sum_{n = 1}^{\infty} \frac{4 n}{n^{2} - 1} \frac{1}{π} \sin (n x), f o r n \in e v e n \end{aligned}