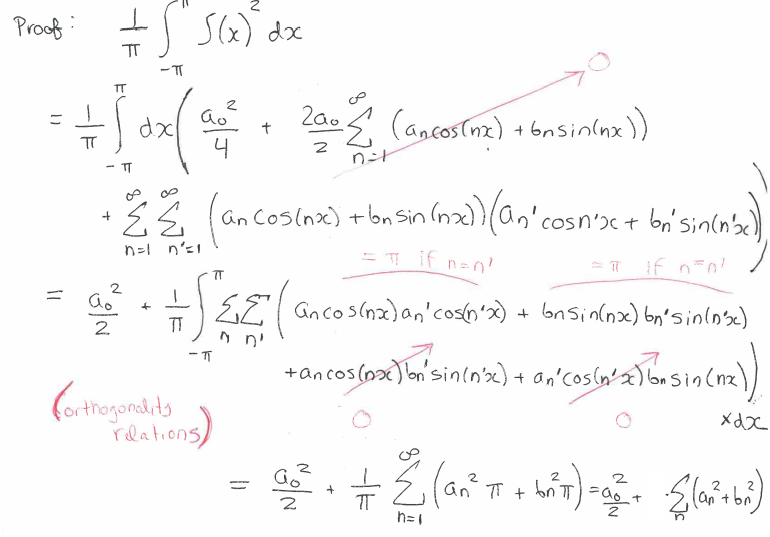PX153 - J6 - parseval's theorem

if $f (x) = \frac{a_{0}}{2} + \sum_{n = 1}^{\infty} (a_{n} \cos (n x) + b_{n} \sin (n x))$ , then, $$\frac{1}{\pi} \int_{-\pi}^{\pi} (f(x))^{2},dx = \frac{a_{0}^{2}}{2} + \sum\limits_{n=1}^{\infty} (a_{n}^{2}+ b_{n}^{2})$$
application in physics: physical waves
if the energy of a wave is the square of the wave function, the sum of $a_{n}^{2}$ , $b_{n}^{2}$ , $\frac{a_{0}^{2}}{2}$ is the sum of the energy of individual vibration modes.

\begin{aligned} \frac{1}{π} \int_{- π}^{π} | f (x) |^{2} d x & = \frac{1}{π} \int_{- π}^{π} [\frac{a_{0}^{2}}{4} + {(\sum_{n} (a_{n} \cos n x + b_{n} \sin n x))}^{2} \\ + 2 \frac{a_{0}}{2} \sum_{n} (a_{n} \cos n x + b_{n} \sin n x)] d x \\ = \frac{1}{π} \int_{- π}^{π} [\frac{a_{0}^{2}}{4} + (\sum_{n} (a_{n} \cos n x + b_{n} \sin n x)) \\ \times (\sum_{n^{'}} (a_{n^{'}} \cos n^{'} x + b_{n^{'}} \sin n^{'} x))] d x \\ = \frac{a_{0}^{2}}{2} + \sum_{n} (a_{n}^{2} + b_{n}^{2}) \end{aligned}