PX153 - J10 - examples

Q1

\begin{aligned} a_{0} & = \frac{1}{L} \int_{- L}^{L} f (x) d x \\ = \frac{1}{1} \int_{0}^{2} x d x \\ = 2 \end{aligned}

\begin{aligned} a_{n} & = \int_{0}^{2} x \cos (\frac{n π x}{L}) d x \\ = {[\frac{x}{n π} \sin (n π x)]}_{0}^{2} - \int_{0}^{2} \frac{1}{n π} \sin (n π x) d x \\ = \frac{1}{(n π)^{2}} [\cos (n π x)]_{0}^{2} \\ = \frac{1}{(n π)^{2}} (\cos (2 n π) - 1) \\ = 0 \end{aligned}

\begin{aligned} b_{n} & = \int_{0}^{2} x \sin (n π x) d x \\ = \frac{1}{n π} ([x \cos (n π x)]_{0}^{2} - \int_{0}^{2} \cos (n π x) d x) \\ = - \frac{2}{n π} + {[\frac{\sin (n π x)}{(n π)^{2}}]}_{0}^{2} \\ = - \frac{2}{n π} \end{aligned}

∴ f (x) = 1 + \sum_{n = 1}^{\infty} (- \frac{2}{n π}) \sin (n π x)

\begin{aligned} a_{0} & = \frac{1}{π} \int_{- π}^{π} \cos (α x) d x \\ = \frac{2}{π} \int_{0}^{π} \cos (α x) d x \\ = \frac{2}{π α} [\sin (α x)]_{0}^{π} \\ = \frac{2}{α π} \sin (α π) \end{aligned}

\begin{aligned} a_{n} & = \frac{1}{π} \int_{- π}^{π} \cos (α x) \cos (n x) d x \\ = \frac{2}{π} \int_{0}^{π} \frac{1}{2} \cos ((α + n) x) + \cos ((α - n) x) d x \\ = \frac{1}{π} {[\frac{\sin ((α + n) x)}{α + n} + \frac{\sin ((α - n) x)}{α - n}]}_{0}^{π} \\ = \frac{1}{π} (\frac{\sin ((α + n) π)}{α + n} + \frac{\sin ((α - n) π)}{α - n}) \end{aligned}

f (x) = {\begin{cases} 0 & x \in [- π, - \frac{π}{2}) \\ 1 & x \in [- \frac{π}{2}, 0) \\ - 1 & x \in [0, \frac{π}{2}) \\ 0 & x \in [\frac{π}{2}, π) \end{cases}

sketch:
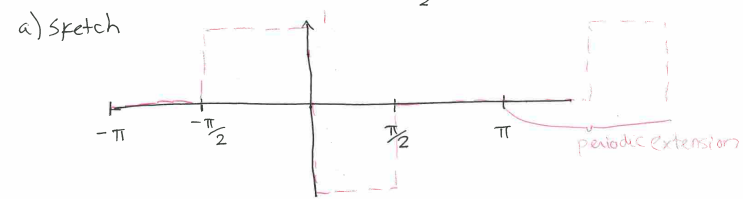
convergence: point-wise
symmetries: anti-symmetric
coefficients and series: $b_{n} = \frac{1}{π} (0 + \int_{- \frac{π}{2}}^{0} 1 \sin (n x) d x - \int_{0}^{\frac{π}{2}} 1 \sin (n x) d x + 0)$
- let $x^{'} = x$ :

\begin{aligned} b_{n} & = \frac{1}{π} (\int_{\frac{π}{2}}^{0} - \sin (n x^{'}) (- d x^{'}) - \int_{0}^{\frac{π}{2}} 1 \sin (n x) d x + 0) \\ = \frac{1}{π} (- \int_{0}^{\frac{π}{2}} \sin (n x) d x - \int_{0}^{\frac{π}{2}} \sin (n x) d x) \\ = - \frac{2}{π} \int_{0}^{\frac{π}{2}} \sin (n x) \\ = - \frac{2}{π} {[- \frac{\cos (n x)}{n}]}_{0}^{\frac{π}{2}} \\ = \frac{2}{π n} {[\cos (\frac{n π}{2}) - 1]}_{0}^{\frac{π}{2}} \end{aligned}

\begin{aligned} n = 1, 5, 9, . . . & : \cos (\frac{π}{2}) = 0 & b_{n} = - \frac{2}{n π} \\ n = 2, 6, 10, . . . & : \cos π = 0 & b_{n} = - \frac{4}{n π} \\ n = 3, 7, 11, . . . & : \cos (\frac{3 π}{2}) = 0 & b_{n} = - \frac{2}{n π} \\ n = 4, 8, 12, . . . & : \cos (2 π) = 0 & b_{n} = 0 \end{aligned}

$f (x) = x$ in $[- π, π)$

sketch:
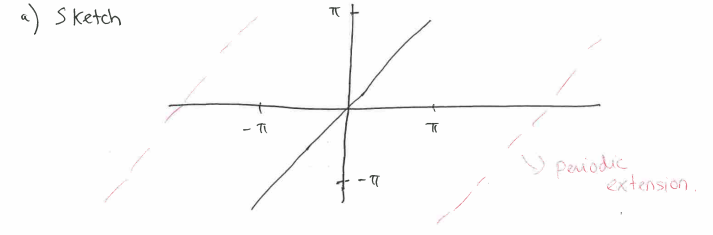
convergence: point-wise (disconitinous at $x = - π$ )
symmetries: anti-symmetric, ie: $a_{0} = 0$ , $a_{n} = 0$
coefficients and series: $$\begin{align*}
b_{n} &= \int_{-\pi}^{\pi} x\sin(nx),dx \
&= \frac{1}{\pi} \left[- \frac{\cos(nx)}{n}x\right]{-\pi}^{\pi} - \frac{1}{\pi} \int{-\pi}^{\pi}- \frac{\cos(nx)}{n}dx \
&= \frac{1}{\pi} \left(- \frac{\pi}{n} (-1)^{n} - \frac{\pi}{n}(-1)^{n} \right) \&= \frac{2}{n} (-1)^{n+1}
\end{align*}$$
fourier series: