PX153 - I4 - non-rectangular domain of integration
- so far, the integration domain has been rectangular, but if the integration region isn't rectangular, then the following approach must be taken
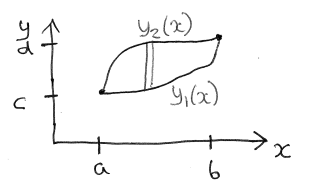
- domain,
, is given by for all - the function is integrated over
from to , and then integrated over from to - can alternatively be thought as:
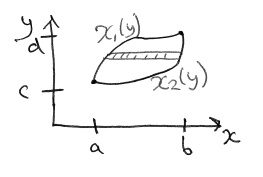
- the function is first integrated over
from to , and then over from to - first way:
- eg:
, , and . evaluate:
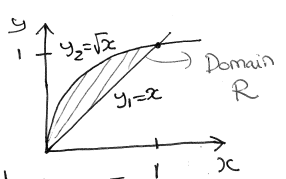
$$I = \int_{0}^{1} \left[ \frac{xy^{3}}{3} \right]{x}^{\sqrt{x}.dx}= \int^{1}(\frac{x^{\frac{5}{2}}}{3}- \frac{x^{4}}{3}).dx =...=\frac{1}{35}$$
- change the order of integration?
$$I= \int_{0}^{1}\left( \int_{x_{1}}^{x_{2}} xy^{2}.dx \right).dy = ... = \frac{1}{35}$$
- eg: find
, where is the domain of integration where the area is enclosed by triangle: , , - first, integrate over
:
- first, integrate over
- can be verified by swapping the order of integration:
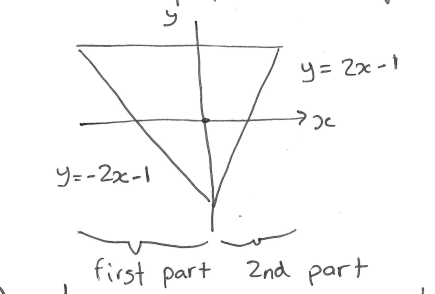
$$I = \int_{-1}^{0} \left( \int_{y_{1}=-2x-1}^{1} (x+y)^{2}.dy \right).dx + \int_{0}^{1} \left( \int_{y_{1}=2x-1}^{1} (x+y)^{2}.dy \right).dx$$
- the result must be
- eg: what is the volume of a sphere of radius,
? - every point at the surface of a sphere:
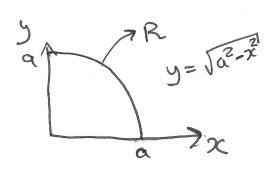
- let,
, , ,
- every point at the surface of a sphere: