PX153 - I1 - introduction

definition

adding up. eg: area under a curve, volume inside a surface, work done from $A$ to $B$ , total electric flux across a surface
inverse of differentiation
if $F (x) = \int^{x} f (x^{'}) . d x^{'}$ , where, $A \to$ some reference point

\begin{aligned} F^{'} (x) & = lim_{δ x \to 0} \frac{F (x + δ x) - F (x)}{δ x} \\ = lim_{δ x \to 0} \frac{\int_{A}^{x + δ x} f (x^{'}) . d x^{'} - \int_{A}^{x} f (x^{'}) . d x^{'}}{δ x} \\ = lim_{δ x \to 0} \frac{\int_{A}^{x + δ x} f (x^{'}) . d x^{'} + \int_{x}^{A} f (x^{'}) . d x^{'}}{δ x} \\ = lim_{δ x \to 0} \frac{\int_{x}^{x + δ x} f (x^{'}) . d x^{'}}{δ x} \\ = lim_{δ x \to 0} \frac{f (x^{'}) δ x}{δ x} \\ = f (x) \end{aligned}

a bit of maths analysis

maths behind differentiation and integration is called analysis and concerned with limits
differentiation, ie:

l i m_{δ x \to 0} \frac{f (x + δ x) - f (x)}{δ x} \overset{?}{=} f^{'} (x)

integral, ie:

lim_{N \to \infty} \sum_{n = 0}^{N} f (x_{A} + n \frac{x_{B} - x_{A}}{N}) \frac{x_{B} - x_{A}}{N} \overset{?}{=} \int_{x_{A}}^{x_{B}} f (x^{'}) . d x^{'}

a) riemann integral

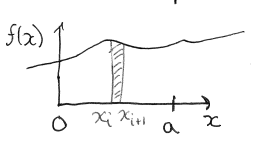
let $A =$ area under the curve (between $0$ and $a$ ):

A \approx \sum_{i = 0}^{N - 1} f (x_{i}) (x_{i + 1} - x_{i})

if the limit $N \to \infty$ exists:

lim_{N \to \infty} \sum_{i = 0}^{N - 1} f (x_{i}) Δ x_{i} = \int_{0}^{a} f (x^{'}) . d x^{'}

we will work with *riemann integral
assume that all functions of interest are integrable
assume that we cab interchange order of integration in multiple integrals (fabini's theorem)
key points:
- integration by parts:

\begin{aligned} \int_{a}^{b} u \frac{d v}{d x} . d x & = \int_{a}^{b} \frac{d (u v)}{d x} . d x - \int_{a}^{b} v \frac{d u}{d x} . d x \\ = [u v]_{a}^{b} - \int_{a}^{b} \frac{d u}{d x} v . d x \end{aligned}

- substitutions:
$$ I = \int \frac{1}{(1-x)^{\frac{1}{2}}}.dx$$
- let $x = \sin u$ , and $d x = \cos u . d u$ :
$$I = \int \frac{\cos u.du}{\cos u} = \int du = u = \sin^{-1} x$$
\1\n\2\n