PX153 - H5 - coordinate systems revisited

extension for circular polar coordinates
in general, in 3D, a coordinate system is defined by specifying 3 basis vectors at each point in space
usually orthonormal basis vectors

\hat{{\vec{e}}_{i}} \cdot \hat{{\vec{e}}_{j}} = δ_{i j}

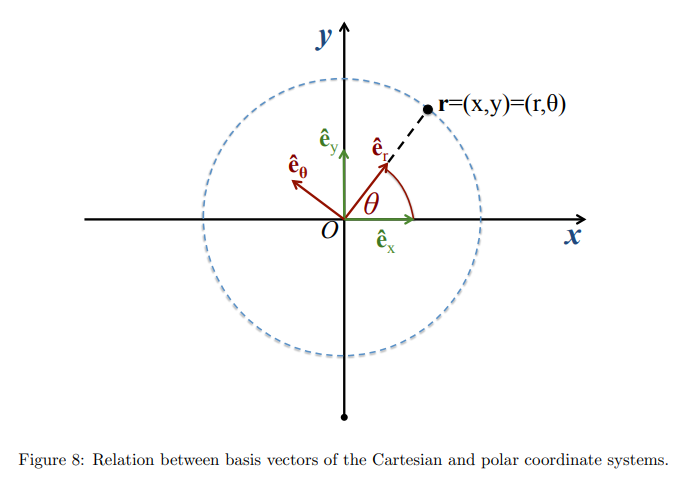
for polar coordinates: $\vec{r} (r, θ)$ , where $r =$ magnitude of the vector, and $θ =$ angle to the x-axis
$x = r \cos θ$
$y = r \sin θ$
$r = \sqrt{x^{2} + y^{2}}$
$θ = \arctan (\frac{x}{y})$
from figure above, and trigonometry:

{\hat{\vec{e}}}_{r} = \cos θ {\hat{\vec{e}}}_{x} + \sin θ {\hat{\vec{e}}}_{y}

{\hat{\vec{e}}}_{θ} = - \sin θ {\hat{\vec{e}}}_{x} + \cos θ {\hat{\vec{e}}}_{y}

\vec{r} = x {\hat{\vec{e}}}_{x} + y {\hat{\vec{e}}}_{y}

{\vec{e}}_{x} = {(\frac{\partial \vec{r}}{\partial r})}_{y} = {\hat{\vec{e}}}_{x}

- ie: basis vectors are in direction of increasing coordinate

{\vec{e}}_{r} = {(\frac{\partial \vec{r}}{\partial r})}_{θ}

{\vec{e}}_{θ} = {(\frac{\partial \vec{r}}{\partial θ})}_{r}

\vec{r} = x {\vec{e}}_{x} + y {\vec{e}}_{y}

- rewriting $x$ and $y$ :
$$\vec r = r \cos\theta ; \vec e_{x} + r\sin\theta ; \vec e_{y}$$

{\vec{e}}_{r} = {(\frac{\partial \vec{r}}{\partial r})}_{θ} = \cos θ {\vec{e}}_{x} + \sin θ {\vec{e}}_{y}

- and,
$$\vec e_{\theta} = \left( \frac{\partial \vec r}{\partial \theta}\right){r} = -r \sin\theta ; \vec e + r \cos\theta ; \vec e_{y}$$

note:
- $| {\vec{e}}_{r} | = 1 ⟹ {\hat{\vec{e}}}_{r} = {\vec{e}}_{r}$ : $$\hat {\vec e}_{r} = \vec e_r$$
- $| {\vec{e}}_{θ} | = r$ :

∴ {\hat{\vec{e}}}_{θ} = \frac{{\vec{e}}_{θ}}{r} = - \sin θ {\hat{\vec{e}}}_{x} + \cos θ {\hat{\vec{e}}}_{y}

\frac{d {\hat{\vec{e}}}_{r}}{d θ} = - \sin θ {\hat{\vec{e}}}_{x} + \cos θ {\hat{\vec{e}}}_{y} = {\hat{\vec{e}}}_{θ}

\frac{d {\hat{\vec{e}}}_{θ}}{d θ} = - \cos θ {\hat{\vec{e}}}_{x} - \sin θ {\hat{\vec{e}}}_{y} = - {\hat{\vec{e}}}_{r}

the position vector in cartesian coordinates is $\vec{r} = x {\hat{\vec{e}}}_{x} + y {\hat{\vec{e}}}_{y}$ , but in polar, it is $\vec{r} = r {\hat{\vec{e}}}_{r}$
eg: circular motion of an object with radius, $r$ , constant angular velocity, $ω r a d s^{- 1}$
- the linear velocity:
$\vec{v} = \frac{d \vec{r}}{d t} = \frac{d}{d t} (r {\hat{\vec{e}}}_{r}) = \dot{r} {\hat{\vec{e}}}_{r} + r {\dot{\hat{\vec{e}}}}_{r}$
- $θ$ is a function of time:
$$\dot{\hat{\vec e}}{r} = \frac{d\hat{\vec e}r}{d\theta} \cdot \frac{d\theta}{dt} = \omega \hat{\vec e}{\theta}$$
- we know $\dot{r} = 0$ :
$$\vec v = \omega r \hat{\vec e}{\theta}$$
- this is a well known result, $v = ω r$ , and direction is tangential
- similarly, acceleration:
$\vec{a} = \frac{d \vec{v}}{d t} = \frac{d}{d t} (ω r {\hat{\vec{e}}}_{θ}) = r ω \frac{d}{d t} {\hat{\vec{e}}}_{θ}$
- we know $θ$ is a function of time:
$\frac{d}{d t} {\hat{\vec{e}}}_{θ} = \frac{d {\hat{\vec{e}}}_{θ}}{d θ} \cdot \frac{d θ}{d t} = - ω {\hat{\vec{e}}}_{r}$ $∴ \vec{a} = - r ω^{2} {\hat{\vec{e}}}_{r}$