PX153 - H4 - application of gradient in physics - the potential of a conservative force

similar to exact and inexact differentials
- a differential is exact if and only if:
$d f = A . d x + B . d y = \frac{\partial f}{\partial x} . d x + \frac{\partial f}{\partial y} . d y$
- such that $\frac{\partial A}{\partial y} = \frac{\partial B}{\partial x}$ , and there is some function, $f (x, y)$ , from which this differential is based
for a conservative field, $\vec{a}$ , there exists a single-values scalar function of position such that $\vec{\nabla} ϕ = \vec{a}$ (equivalent to $\vec{a} \cdot d \vec{r}$ is an exact differential), and the integral along a path between two points $\int_{A}^{B} \vec{a} \cdot d \vec{r}$ does not depend on the path taken
eg: consider two charges, $q_{1}$ and $q_{2}$ , separated by a distance, $r$ , with $q_{1}$ at the origin
- the potential energy is given by:
$U (r) = \frac{q_{1} q_{2}}{4 π ϵ_{0} r} = \frac{q_{1} q_{2}}{4 π ϵ_{0}} \cdot \frac{1}{\sqrt{x^{2} + y^{2} + z^{2}}}$

\vec{\nabla} U (x, y, z) = \frac{q_{1} q_{2}}{4 π ϵ_{0}} (\begin{matrix} \frac{- 2 x}{2 (x^{2} + y^{2} + z^{2})^{\frac{3}{2}}} \hat{\vec{i}} \\ - \frac{y}{2 (x^{2} + y^{2} + z^{2})^{\frac{3}{2}}} \hat{\vec{j}} \\ - \frac{z}{2 (x^{2} + y^{2} + z^{2})^{\frac{3}{2}}} \hat{\vec{k}} \end{matrix})

recall: $\hat{\vec{r}} = \frac{1}{\sqrt{(x^{2} + y^{2} + z^{2}}} [x \hat{\vec{i}} + y \hat{\vec{j}} + z \hat{\vec{k}}]$ $\vec{\nabla} U = - \frac{q_{1} q_{2}}{4 π ϵ_{0} r^{2}} \hat{\vec{r}} = - \vec{F}$
coulomb force on $q_{2}$ due to $q_{1}$ :

\vec{F} = - \vec{\nabla} U (x, y, z)

forces can be described as gradients of potentials are called conservative forces
the work done by a conservative force is given by the potential difference between the start( $A$ ), and the end( $B$ ), independent of the path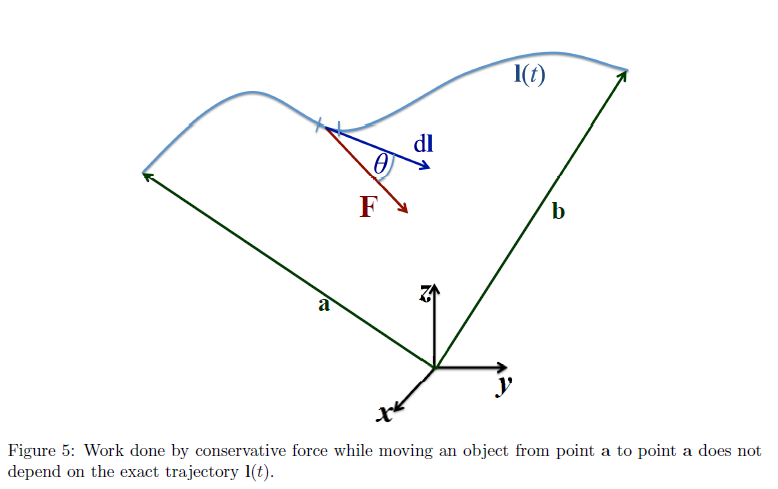
we have:

W = F l \cos θ

d W = \vec{F} \cdot d \vec{l}

W = \int_{A}^{B} \vec{F} . d \vec{l}

\vec{l} (t) = x (t) \hat{\vec{i}} + y (t) \hat{\vec{j}} + z (t) \hat{\vec{k}}

W = \int_{t_{A}}^{t_{B}} \vec{F} \frac{d \vec{l}}{d t} . d t

assuming the force is conservative: $F = - \vec{\nabla} U$ , and using $\frac{d \vec{l}}{d t} = (\frac{d x}{d t}, \frac{d y}{d t}, \frac{d x}{d t})$ :

W = \int_{t_{A}}^{t_{B}} - \vec{\nabla} U \frac{d \vec{l}}{d t} . d t

W = - \int_{t_{A}}^{t_{B}} (\frac{\partial U}{\partial x} \frac{d x}{d t} + \frac{\partial U}{\partial y} \frac{d y}{d t} + \frac{\partial U}{\partial z} \frac{d z}{d t}) . d t

\frac{d U}{d t} = \frac{\partial U}{\partial x} \frac{d x}{d t} + \frac{\partial U}{\partial y} \frac{d y}{d t} + \frac{\partial U}{\partial z} \frac{d z}{d t}

W = - \int_{t_{A}}^{t_{B}} \frac{d U}{d t} . d t = - \int_{A}^{B} d U

W = U (A) - U (B)

- ie: work done does not depend on the the path for a conservative field

showing how to determine a scalar field from a conservative vector field
eg: find the scalar function $U (x, y, z)$ , for which the vector function: $\vec{a} = - \vec{\nabla} U = - 2 x \hat{\vec{i}} - 2 y \hat{\vec{j}} - 2 z \hat{\vec{k}}$ , and such that $U (0, 0, 9) = 0$
- exact differential?
  - $\vec{a} \cdot d \vec{r} = - 2 x d x - 2 y d y - 2 z d z$
  - if $A_{y} = B_{x}$ , $B_{z} = C_{y}$ , and $C_{x} = A_{z}$
$- \frac{\partial U}{\partial x} = - 2 x ⟹ U = x^{2} + F_{x} (y, z)$ $- \frac{\partial U}{\partial y} = - 2 x ⟹ U = y^{2} + F_{y} (x, z)$ $- \frac{\partial U}{\partial z} = - 2 z ⟹ U = z^{2} + F_{z} (x, y)$ $U (x, y, z) = x^{2} + y^{2} + (z - 9)^{2} + c$ $U (0, 0, 9) = 0 ⟹ c = 0$ $∴ U (x, y, z) x^{2} + y^{2} + (z - 9)^{2}$