PX153 - H3 - gradients of functions of three variables

• $f(x,y,z)=\kappa$ represents contours as planes of constant value
• gradient vector:

- perpendicular to the planes of constant value

• this gives us a convenient way of finding a vector perpendicular to a surface:

• eg: $f(x,y,z)=x^2+y^2+z^2$

  • surfaces of constant value are spheres
  $$f(x,y,z)=\kappa =x^2+y^2+z^2$$
  • sphere of radius $\sqrt{\kappa }$ centred on $x=y=z=0$
  $$\overrightarrow{\mathrm{\nabla }}f=2x\hat{\overrightarrow{i}}+2y\hat{\overrightarrow{j}}+2z\hat{\overrightarrow{k}}=\overrightarrow{r}$$$$\hat{\overrightarrow{n}}=\frac{\overrightarrow{r}}{|\overrightarrow{r}|}$$

  - in spherical polar coordinates

• eg: find the vector normal to the surface of a torus
  
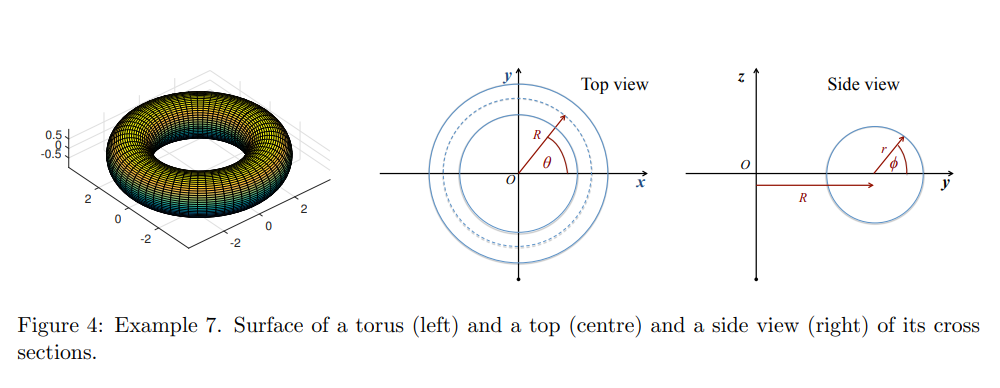
  $R=$ major radius, $r=$ minor radius
  $\theta =$ toroidal angle ($R$), $\varphi =$ poloidal angle ($r$)
  $x=(R+r\cos \varphi )\cos \theta$
  $y=(R+r\cos \varphi )\sin \theta$
  $z=R\sin \varphi$
  need to eliminate $\theta ,\varphi$:

• describes the surface of the torus i cartesian coordinates

• now, find the normal to vector from $\overrightarrow{\mathrm{\nabla }}f$:
  $$ \frac{\partial f}{\partial x} = 2(\sqrt{x^{2}+ x^{2}}- R^{2}) \frac{x}{\sqrt{x^{2}+y^{2}}}$$
  $$ \frac{\partial f}{\partial x} = 2(\sqrt{x^{2}+ y^{2}}- R^{2}) \frac{y}{\sqrt{x^{2}+y^{2}}}$$
  $$ \frac{\partial f}{\partial z} = 2z$$
  $$\vec\nabla f = 2x \frac{(\sqrt{x^{2}+ x^{2}}- R^{2})}{\sqrt{x^{2}+y^{2}}} \hat{\vec i} + 2y \frac{(\sqrt{x^{2}+ x^{2}}- R^{2})}{\sqrt{x^{2}+y^{2}}} \hat{\vec k} + 2z \hat{\vec k}$$