PX153 - H2 - visualising variability of a scalar function - contours

• contours - eg think of height, $z$, as a function of position int he $x,y$ plane, ie: $z(x,y)$

• contour lines mark out lines of constant height, ie: defined by $z(x,y)=k$ , where $k$ is a constant

• we will show that the direction of greatest rate of change is perpendicular to the contour

• consider two contour lines that are close together, ie: $f(x,y)={\kappa }_1$ , and $f(x,y)={\kappa }_2$ , where ${\kappa }_2={\kappa }_1+\delta \kappa$ , and $\delta \kappa$ is small

• consider the rate of change along $A\to B$, where $A\to B$ is perpendicular to the contour, compared to the rate of change along $A\to C$
  $\mathrm{\Delta }n=AB$ , and $\mathrm{\Delta }r=AC$
  $\mathrm{\Delta }n=\mathrm{\Delta }r\cos \theta$

• for infinitesimally small changes:

• the change in $f$, $\mathrm{\Delta }f$, between $A$ and $B$ is the same as between $A$ and $C$. so, the rate is determined just by the length
• thus, the directional derivative, given by $\overrightarrow{\mathrm{\nabla }}f=\frac{\partial f}{\partial n}\hat{n}$ , gives the highest change of $f$ and is always perpendicular to the contour of constant $f$. this gives a geometrical definition of $\overrightarrow{\mathrm{\nabla }}f$
• we would show shortly that this is equivalent to our previous definition:

• eg: for $f(x,y)$, find $\overrightarrow{\mathrm{\nabla }}f$, evaluate the gradient at $(\frac{1}{2},\frac{1}{2})$ , and hence find the direction of the fastest change in $f$ at that point

  • for gradient:
  $$\overrightarrow{\mathrm{\nabla }}f=(\hat{i}\frac{\partial }{\partial x}+\hat{j}\frac{\partial }{\partial y})f=\hat{\overrightarrow{i}}-\hat{\overrightarrow{j}}$$
  • at all points, gradient is $(1,-1)$, magnitude $\sqrt{2}$, and direction $\frac{1}{\sqrt{2}}(1,-1)$
  • the contour lines are:
  $$f(x,y)=\kappa =x-y⟹y=x-\kappa$$

  

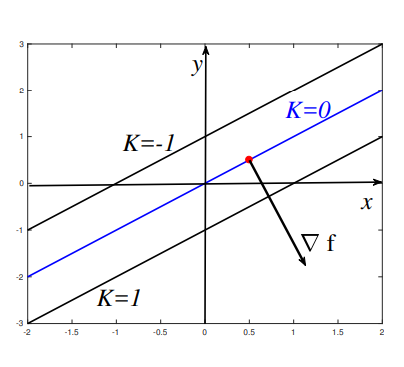
• eg: at $(1,2)$ find the direction along which $f(x,y)=x^{2}y+xy$ changes most rapidly

  • taking the directional derivative:
  $$\overrightarrow{\mathrm{\nabla }}f=(2xy+y)\hat{\overrightarrow{i}}+(x^2+x)\hat{\overrightarrow{j}}$$
  • at $(1,2)$: $\overrightarrow{\mathrm{\nabla }}f(1,2)=6\hat{\overrightarrow{i}}+2\hat{\overrightarrow{j}}$
  • the direction is given by
  $$\hat{\overrightarrow{u}}=\frac{\overrightarrow{\mathrm{\nabla }}f}{|\overrightarrow{\mathrm{\nabla }}f|}=\frac{3}{\sqrt{10}}\hat{\overrightarrow{i}}+\frac{1}{\sqrt{10}}\hat{\overrightarrow{j}}$$

• we now show that $\overrightarrow{\mathrm{\nabla }}f=(\frac{\partial }{\partial x}\hat{\overrightarrow{i}}+r\hat{\overrightarrow{j}}\frac{\partial }{\partial y})f$ is perpendicular to the tangent of the contour line of $f$, consistent with our geometrical definition

• let $f(x,y)=\kappa$ define a contour, which is parameterized by $q$, ie: all points on this contour are given by $\overrightarrow{r}(q)=[x(q),y(q)]$

• varying $q$ takes us aroufd this contour, on which the function assumes an arbitrary constant value $\kappa$, thus:

- this derivative can be rewritten as:
$$df = \frac{\partial f}{\partial x} dx + \frac{\partial f}{\partial y} dy \implies \frac{df}{dq} = \frac{\partial f}{\partial x} \frac{dx}{dq} + \frac{\partial f}{\partial y} \frac{dy}{dq}$$
- can write this as a scalar product:
$$\frac{df}{dq}= (\frac{\partial f}{\partial x},\frac{\partial f}{\partial y})\cdot ( \frac{dx}{dq}, \frac{dy}{dq})$$

• the vector $\overrightarrow{t}=(\frac{dx}{dq},\frac{dy}{dq})=\frac{d}{dq}\overrightarrow{r}$ is the direction of the tangent to the contour:

• eg: what are the shapes of the contour lines of the function, $f(x,y)=e^{-(x^2+y^2)}$? find the general expression for the gradient
  • contour lines are defined by $f(x,y)=\kappa =e^{-(x^2+y^2)}$
    $⟹x^2+y^2=\ln (\frac{1}{\kappa })$
    • ie: circles of radius $\sqrt{\ln \frac{1}{\kappa }}$ centred on the origin
  • the gradient is given by:
  $$\overrightarrow{\mathrm{\nabla }}f=(-2x{e}^{-(x^2+y^2)})\hat{\overrightarrow{i}}+(-2y{e}^{-(x^2+y^2)})\hat{\overrightarrow{j}}$$

\1\n\2\n