PX153 - D3 - reducing a non-linear ODE to a linear ODE

non-linear ODEs are usually very difficult or impossible to solve, so, we try to make assumptions to simplify them
here, we give the example of a pendulum
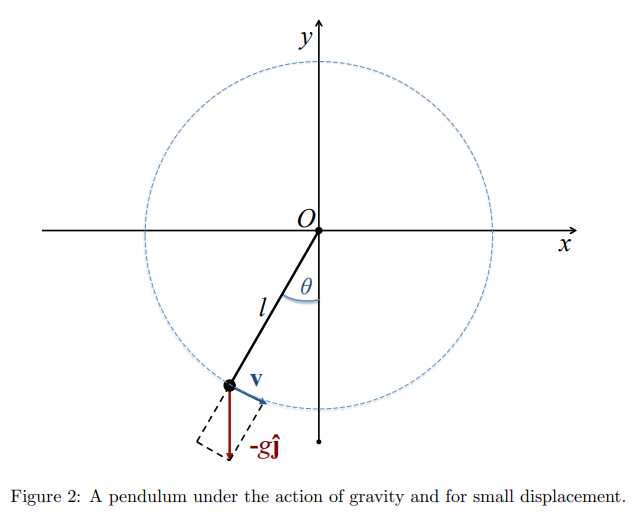
the length of arc $d s$ travelled in $d t$ is related to the change in the angle $d θ$ : $d s = l d θ$
so the acceleration is $\frac{d^{2} s}{d t^{2}} = l \frac{d^{2} θ}{d t^{2}}$
this must be equal to the component of the gravity tangential to the trajectory $- m g \sin θ$
giving: $m l \frac{d^{2} θ}{d t^{2}} = - m g \sin θ$
$$\frac{d^{2}\theta}{dt^{2}} = - \frac{g}{l}\sin\theta$$
- this is non-linear and very tough to solve
to simplify the differential, we make a small angle approximation, such that $\sin θ \approx θ$ : $$\frac{d^{2}\theta}{dt^{2}} \simeq - \frac{g}{l}\theta$$