PX153 - B5 - application - describing damped smh

general solution

conder mass on a spring on a surface to give a friction force proportional to the speed of the mass
the equation of motion becomes:

m \frac{d^{2} x}{d t^{2}} = - k x - γ \frac{d x}{d t}

rearrange:

\frac{d^{2} x}{d t^{2}} + \frac{γ}{m} \frac{d x}{d t} + \frac{k}{m} x = 0

rewrite:

\frac{d^{2} x}{d t^{2}} + 2 α \frac{d x}{d t} + ω_{0}^{2} x = 0

where, $α = \frac{γ}{2 m}$ , $ω_{0} = \sqrt{\frac{k}{m}}$

try $x (t) = A e^{λ t}$ :

λ^{2} + 2 α λ + ω_{0}^{2} = 0

- quadratic equation, two solutions:
$$\lambda_{1}=-\alpha+\sqrt{\alpha^{2}-\omega_{0}^{2}} , ,, and , , \lambda_{2}=-\alpha-\sqrt{\alpha^{2}-\omega_{0}^{2}}$$
- the general solution:
$$x(t)=Ce^{\lambda_{1}t}+De^{\lambda_{2}t}$$
$$x(t)= e^{-\alpha t}(Ce^{t\sqrt{\alpha^{2}-\omega_{0}^{2}}}+De^{-t\sqrt{\alpha^{2}-\omega_{0}^{2}}})$$
- first, the damping/dissipative force acts to make the displacement decay over time ( $e^{- α t}$ , $α \in R$ )
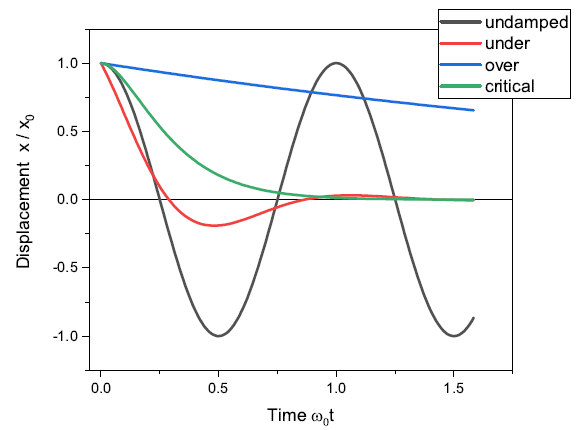
- three cases:
- case 1: $α^{2} < ω_{0}^{2}$ - PX153 - B5.1 - underdamping
- case 2: $α^{2} > ω_{0}^{2}$ - PX153 - B5.2 - overdamping
- case 3: $α^{2} = ω_{0}^{2}$ - PX153 - B5.3 - critical damping