PX153 - A4 - vector operations
addition and subtraction
- properties
- commutative -
- associative -
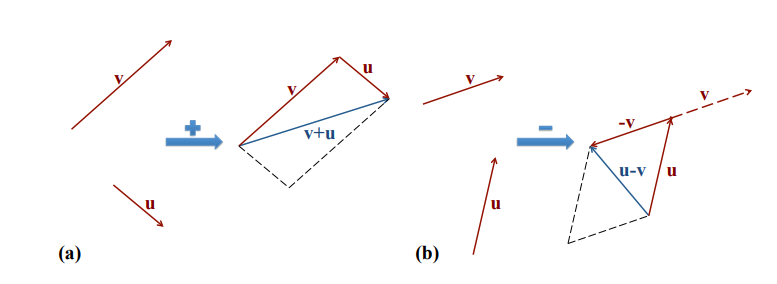

- commutative -
vector products
scalar/dot product
is a scalar
- geometrically, it is the magnitude of one vector projected on the other
-
- if
(orthogonal vectors), - for cartesian coordinate basis vectors
and
$$\underline{\hat i}\cdot \underline{\hat j}=\underline{\hat j}\cdot \underline{\hat k}=\underline{\hat k}\cdot \underline{\hat i}=0$$
- this denotes that the basis vectors are orthonormal
- properties
- commutative -
- distributive -
- commutative -
- in cartesian coordinates -
- using both definitions:
- component of
along
- component of
- eg of scalar product in physics:
vector/cross product
-
is a vector
-
geometrically,
and define a parallelepiped of area
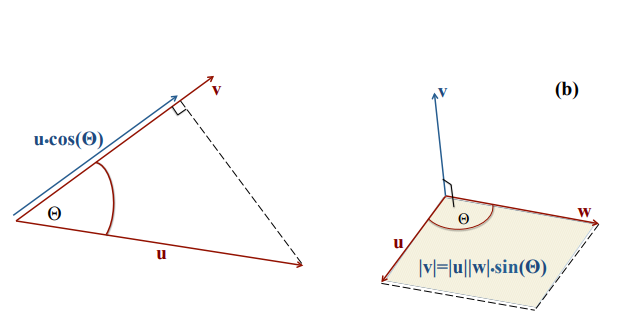
-
is a vector perpendicular to the plane of and - magnitude
- direction is set by the right-hand rule $$\vec v = uw\sin{\theta}\underline{\hat e}_v$$
is the same independent of the coordinate system, its component in a given basis changes
- magnitude
-
cases
- if
and are parallel, and - if
and are not parallel,
- if
-
for cartesian coordinates,
, ,
-
properties:
- vector product is NOT commutative, ie:
- it is anti-commutative, ie:
- vector product is NOT commutative, ie:
-
calculating cross product:$$\vec v = \vec u \times \vec w = (u_yw_z-u_zw_y)\underline{\hat i}+(\vec u_zw_x-u_xw_z)\underline{\hat j}+(\vec u_xw_y-u_yw_x)\underline{\hat k}$$
- easy tip:
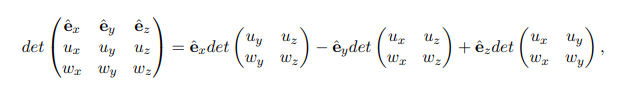
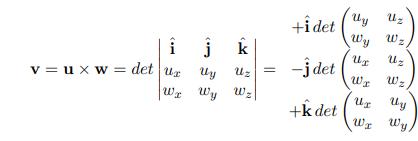

- easy tip:
-
many physical quantities are defined by cross product
- eg:, angular momemtum -
eg of cross product calculation