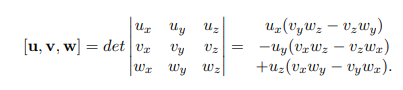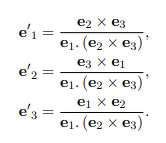PX153 - A0

A1

vectors

quantities with magnitude and direction
- magnitude:

v = | \vec{v} | = \sqrt{v_{x}^{2} + v_{y}^{2} + v_{z}^{2}}

- direction:

\underset{―}{\hat{v}} = \frac{\vec{v}}{| \vec{v} |}

change in coordinate system will change the vector (doesn't change scalar)

vector fields

describes vector that varies continuously in space

A2

basis vectors

3 linearly independent, usually orthonormal vectors used to define the projection of a vector along their respective directions

\vec{v} = (\underset{―}{{\hat{v}}_{x}}, \underset{―}{{\hat{v}}_{y}}, \underset{―}{{\hat{v}}_{z})} = v_{x} \underset{―}{{\hat{e}}_{x}} + v_{2} \underset{―}{{\hat{e}}_{y}} + v_{3} \underset{―}{{\hat{e}}_{z}}

\vec{v} = \sum_{i = x, y, z} v_{i} \underset{―}{{\hat{e}}_{i}}

direction of $\vec{v}$ :

\underset{―}{\hat{v}} = \frac{v_{x}}{| \vec{v} |} \underset{―}{{\hat{e}}_{x}} + \frac{v_{y}}{| \vec{v} |} \underset{―}{{\hat{e}}_{y}} + \frac{v_{z}}{| \vec{v} |} \underset{―}{{\hat{e}}_{z}}

direction cosines

relate to the components of $\vec{v}$ to the its angle relative to the cartesian basis vectors

c o s α = \frac{v_{x}}{| \vec{v} |}, c o s β = \frac{v_{y}}{| \vec{v} |}, c o s γ = \frac{v_{z}}{| \vec{v} |}

A3

position vectors

position of a point with respect to the origin
usually $\vec{r}$

\vec{r} (P) = (r_{x}, r_{y}, r_{z})

describing motion

position

\vec{r} (t) = x (t) \underset{―}{\hat{i}} + y (t) \underset{―}{\hat{j}} + z (t) \underset{―}{\hat{k}}

velocity

\vec{v} (t) = \frac{d \vec{r} (t)}{d t}

acceleration

\vec{a} (t) = \frac{d \vec{v} (t)}{d t} = \frac{d^{2} \vec{r} (t)}{d t^{2}}

equations of motion in vector form

\vec{F} = m \vec{a} = m \vec{g}

\vec{a} = \frac{d^{2} r}{d t^{2}} = - g \underset{―}{\hat{j}} = \frac{d \vec{v}}{d t} . . . (i)

\vec{v} (t) = {\vec{v}}_{0} + \int_{0}^{t} \frac{d \vec{v}}{d t} d t = {\vec{v}}_{0} + \int_{0}^{t} - g \underset{―}{\hat{j}} . d t . . . f r o m [i]

\vec{v} = {\vec{v}}_{0} - g t \underset{―}{\hat{j}}

\vec{r} (t) = {\vec{r}}_{0} + \int_{0}^{t} \vec{v} (t) . d t $ $ $ $ \vec{r} (t) = {\vec{r}}_{0} + {\vec{v}}_{0} t - \frac{1}{2} g t^{2} \underset{―}{\hat{j}}

the components:
- $x (t) = v_{0 x} t$
- $y (t) = h_{0} + v_{0 y} t - \frac{1}{2} g t^{2}$

A4

vector operations

addition and subtraction

\vec{u} \pm \vec{v} = (u_{x} \pm v_{x}, u_{y} \pm v_{y}, u_{z} \pm v_{z})

properties:
- commutative
- associative

multiplication

scalar/dot product

s = \vec{u} \cdot \vec{v}

geometric definition: magnitude of one product projected on the other

s = \vec{u} \cdot \vec{v} = | \vec{u} | | \vec{v} | \cos θ

in cartesian coordinates

s = \vec{u} \cdot \vec{v} = u_{x} v_{x} + u_{y} v_{y} + u_{z} v_{z}

component of $\vec{u}$ along $\vec{v}$ $= {\vec{u}}_{v} = (\frac{\vec{u} \cdot \vec{v}}{v^{2}}) \vec{v} = (\frac{\vec{u} \cdot \vec{v}}{v}) \underset{―}{\hat{v}}$
cases:
- if $s = 0$ , vectors are perpendicular
$\underset{―}{\hat{i}} \cdot \underset{―}{\hat{j}} = \underset{―}{\hat{j}} \cdot \underset{―}{\hat{k}} = \underset{―}{\hat{k}} \cdot \underset{―}{\hat{i}} = 0$
- if $s = u v$ , vectors are parallel
$\underset{―}{\hat{i}} \cdot \underset{―}{\hat{i}} = \underset{―}{\hat{j}} \cdot \underset{―}{\hat{j}} = \underset{―}{\hat{k}} \cdot \underset{―}{\hat{k}} = 1$
- if $s = - u v$ , vectors are anti-parallel
properties:
- commutative
- distributive

vector/cross product

\vec{v} = \vec{u} \times \vec{w}

geometric definition:
- $\vec{v}$ is perpendicular to the plane of $\vec{u}$ and $\vec{w}$
- $v = u w \sin θ$
calculation:

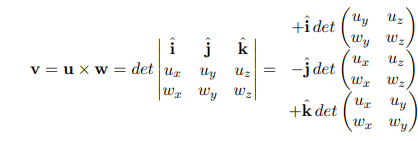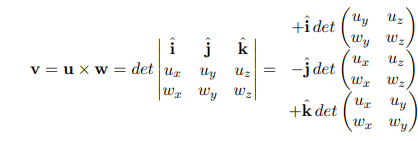\vec v = \vec u \times \vec w = (u_yw_z-u_zw_y)\underline{\hat i}+(\vec u_zw_x-u_xw_z)\underline{\hat j}+(\vec u_xw_y-u_yw_x)\underline{\hat k}$$or, ![Pasted image 20231009190210.png](/img/user/pics/Pasted%20image%2020231009190210.png) - cases: - if $\vec u$ and $\vec w$ are parallel, $\theta = 0$ and $\vec u \times \vec w = 0$ - if $\vec u$ and $\vec w$ are not parallel, $\vec u \cdot(\vec u \times \vec w) = 0$ - properties: -anti-commutative## A5 ### coordinate systems -cartesian coordinates-polar coordinates$$(r,\theta)

where, $r = \sqrt{x^{2} + y^{2}}$ ; $θ = \arctan \frac{y}{x}$
- basis vectors vary but are always orthonormal
$\underset{―}{{\hat{e}}_{r}} = \cos θ \underset{―}{{\hat{e}}_{x}} + \sin θ \underset{―}{{\hat{e}}_{y}}$
$\underset{―}{{\hat{e}}_{θ}} = - \sin θ \underset{―}{{\hat{e}}_{x}} + \cos θ \underset{―}{{\hat{e}}_{y}}$